Dynamical spin ice

J. Xu, Owen Benton, V. K. Anand, A. T. M. N. Islam, T. Guidi, G. Ehlers, E. Feng, Y. Su, A. Sakai, P. Gegenwart, and B. Lake, Anisotropic exchange Hamiltonian, magnetic phase diagram, and domain inversion of Nd₂Zr₂O₇, Phys. Rev. B 99, 144420 (2019)

Spin ice , water ice and inelastic neutron scattering data and simulations.

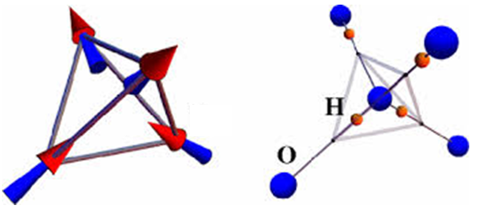
Ice could be the most common substance in our life. However, it has many striking physical properties. For example, the density of ice is approximately 90% of water in contrast to many other matter and violates the general thermal expansion rules. The reason behind is the formation hydrogen bond in water ice which is directional, strong and shorter than the sum of the O^2- and H⁺ radii. Another remarkable phenomenon is the missing H⁺ periodic pattern in water ice at very low temperatures near absolute zero, inducing residual entropy which violates the second law of thermal dynamics. In crystalline water ice, a O^2- ion is surrounded by four H⁺ ions and then four H⁺ ions on the vertex of a tetrahedron (see the figures). Because the O^2--O^2- distance is larger than two times of the hydrogen bond length. There two out of four nearest H⁺ ions are closer to the central O^2- and two further. There six such patterns for a tetrahedron and nearly infinite for a whole block of water ice.

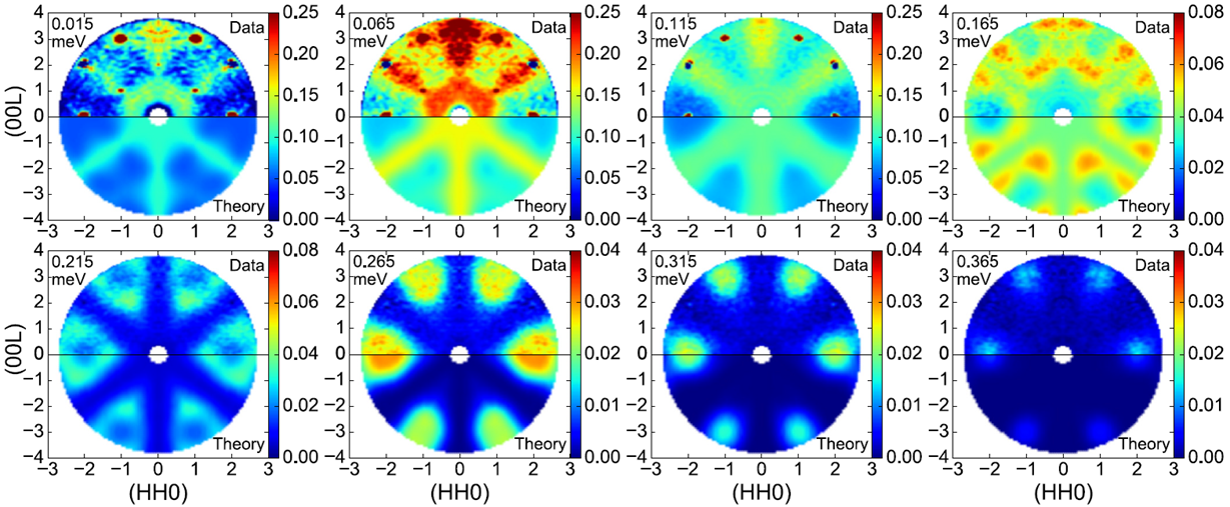
In magnetic material, there is an analog which is called spin ice, where the magnetic moments carried by some ions on the vertex of tetrahedra forming a “two-in-two-out” pattern. In this paper, we studied the candidate material Nd₂Zr₂O₇ for spin ice by thermodynamic and neutron-scattering measurements. Several theoretical methods were used to determined the anisotropic exchange Hamiltonian (mean field approximation, linear spin-wave theory, numerical linked-cluster expansion and Monte Carlo simulations.