Jianhui Xu

Jianhui Xu

PhD in Physics

Easy parking

Introduction

I am very excited to have completed my driving lessons and obtained my driving license (Category B vehicles with a manual gearbox) in Germany. I am very proud to have passed the exams on my first attempt, which also saved me some money, especially considering the nearly 40% failure rate for both the practical and theoretical tests.

Many people find it challenging to squeeze a car into a parking space in the city. One needs to be patient and keep practicing the techniques taught by the driving school instructor. However, these techniques can vary depending on the vehicle, and the actual situation changes every time. Out of a strong curiosity and a desire to park a car as precisely as possible, I did some research on car steering and would like to share some tips for easy parking.

Understanding Car Steering

We all know that：

  1. The front wheels can be turned to the sides, while the rear wheels remain fixed parallel to the vehicle. This is why it is easier to reverse into a parking space to get the inflexible rear end in first.
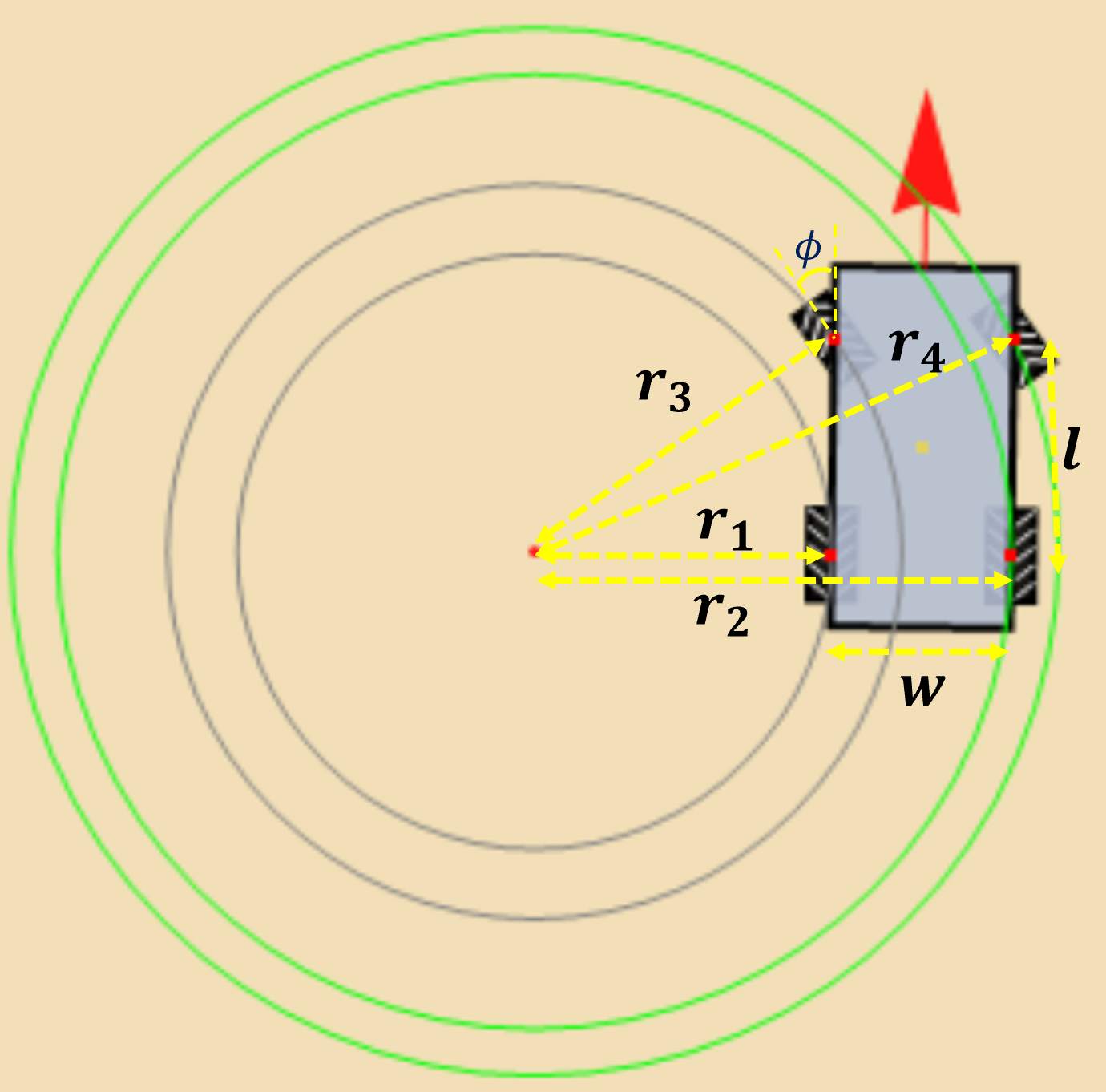
  2. When turning, the four wheels follow different circular paths, each with a different radius. The radius depends on the steering angle, the distance between the front and rear axles, and the width of the car.
  3. The turning radius for the inner rear wheel (\(r_1\)) is the smallest, which often causes accidents.

Assuming \(\phi\) is the steering angle, l is the distance between the front and rear wheels, and \(w\) is the width of the car, the turning radii for the four wheels are given by:

  1. Inner rear: \(r_1 =l\cot(\phi)\)
  2. Outer rear: \(r_2 = r_1 + w\)
  3. Inner front: \(r_3= r1/\cos(\phi)\)
  4. Outer front: \(r_4 = \sqrt{r_2^2 + l^2}\)
The turning radii
The turning radii for the four wheels.

Visualizing Car Steering with Mathematica

I wrote some codes in Mathematica based on the work of Jaime Rangel-Mondragon. I added the turning circles for the four wheels, and the path of movement. I found these visualizations to be very helpful for understanding car steering.

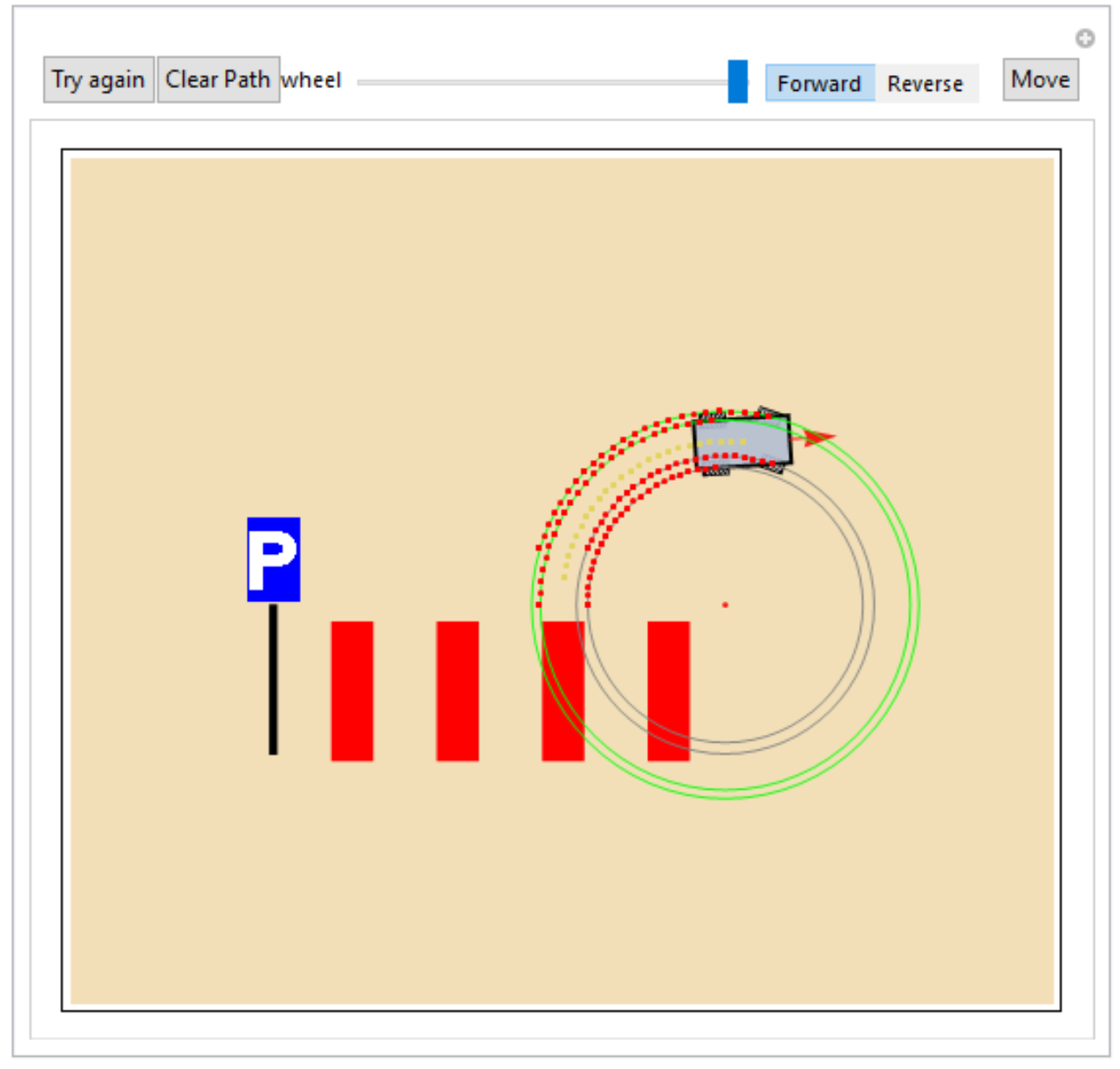
this is a placeholder image
The concentric turning circles of different radii for different wheels.
Mathematica code 
  

wheel[c_, e_] := Module[{d, f, g, h, \[Lambda]},
  {d, f} = {c + e + .5 ({{0, -1}, {1, 0}}.e), 
    c + e - .5 ({{0, -1}, {1, 0}}.e)};
  {g, h} = {2 c - f, 2 c - d};
  {Black, Polygon[{g, d, f, h}], White, 
   Table[Line[{\[Lambda] d + (1 - \[Lambda]) g, (\[Lambda] + .2) (d + 
           f)/2 + (.8 - \[Lambda]) (g + h)/
         2, \[Lambda] f + (1 - \[Lambda]) h}], {\[Lambda], 
     0, .8, .2}]}]

(*van[PosOfFrontMedEdge,PosOfRearMedEdge,AbsOrientationVectorOfWheel]*)

van[a_, b_, e2_] := Module[{e1 = .25 (b - a), d, f, g, h, i, j, k, l},
  {d, f} = {a + {{0, -1}, {1, 0}}.e1, a - {{0, -1}, {1, 0}}.e1};
  {g, h} = {b + d - a, b - d + a};
  {i, j} = {.8 d + .2 g, .8 g + .2 d};
  {k, l} = {i + f - d, j + f - d};
  {EdgeForm[Thick], wheel[i, e2], wheel[k, e2], wheel[j, .5 e1], 
   wheel[l, .5 e1], ColorData[2, 6], Polygon[{d, f, h, g}]}]
wheelPositions[a_, b_, e2_] := 
 Module[{e1 = .25 (b - a), d, f, g, h, i, j, k, l},
  {d, f} = {a + {{0, -1}, {1, 0}}.e1, a - {{0, -1}, {1, 0}}.e1};
  {g, h} = {b + d - a, b - d + a};
  {i, j} = {.8 d + .2 g, .8 g + .2 d};
  {k, l} = {i + f - d, j + f - d};
  {i, k, j, l}]
circles[a_, b_, di_] := Module[
  {e1 = .25 (b - a), d, f, g, h, i, j, k, l, axD, axW, r1, r2, r3, r4,
   t = Arg[
     I (b[[2]] - a[[2]]) + (b[[1]] - 
        a[[1]])](*use this t and these centers, "try again" works*)
   },
  {d, f} = {a + {{0, -1}, {1, 0}}.e1, a - {{0, -1}, {1, 0}}.e1};
  {g, h} = {b + d - a, b - d + a};
  {i, j} = {.8 d + .2 g, .8 g + .2 d};
  {k, l} = {i + f - d, j + f - d};
  axD = Norm[i - j]; 
  axW = Norm[
    f - d];(*distance between front and rear axes and axis width*)
  (*Turn radii for the  four wheels: inner rear, innter frout, 
  outer rear, outer front*)
  r1 = axD Abs[ Cot[di]]; r2 = r1/Abs[Cos[di]]; r3 = r1 + axW; 
  r4 = Sqrt[r3^2 + axD^2];
  (*Circles which the wheels are on when turning, 
  the commented ones only work for right turns (positive di)*)
  {Gray,
   Circle[center[a, b, di], Abs[r1]],(*Circle[{-r1 Sin[t],r1 Cos[t]}+
   j,Abs[r1]],*)
   Circle[center[a, b, di], Abs[r2]],(*Circle[{-r2 Sin[t-di],r2 Cos[t-
   di]}+i,Abs[r2]],*)
   Green,
   (*the rear left wheel*)
   Circle[center[a, b, di], Abs[r3]],(*Circle[{-r3 Sin[t],r3 Cos[t]}+
   l,Abs[r3]],*)
   (*the front left wheel*)
   Circle[center[a, b, di], Abs[r4]],(*Circle[{-r3 Sin[t],r3 Cos[t]}+
   l,Abs[r4]]*),
   Red,
   Point[center[a, b, di]]}
  (*Point[{{-r1 Sin[t],r1 Cos[t]}+j,{-r2 Sin[t-di],r2 Cos[t-di]}+
  i}]}*)
  ]
center[a_, b_, di_] := 
 Module[{e1 = .25 (b - a), d, f, g, h, i, j, k, l, axD, r1, r2,
   t = Arg[I (b[[2]] - a[[2]]) + (b[[1]] - a[[1]])]},
  {d, f} = {a + {{0, -1}, {1, 0}}.e1, a - {{0, -1}, {1, 0}}.e1};
  {g, h} = {b + d - a, b - d + a};
  {i, j} = {.8 d + .2 g, .8 g + .2 d};
  {k, l} = {i + f - d, j + f - d};
  axD = Norm[i - j];
  r1 = axD Cot[di]; r2 = Abs[axD/Sin[di]];
  If[di >= 0,
   {-r2 Sin[t - di], r2 Cos[t - di]} + 
    i, {r2 Sin[t - di], -r2 Cos[t - di]} + 
    k](*different steer directions, different centers: {right side, 
  left side}*)
  ]
radious[a_, b_, di_] := Module[
  {e1 = .25 (b - a), d, f, g, h, i, j, k, l, axD, axW, r1, r2, r3, r4},
  {d, f} = {a + {{0, -1}, {1, 0}}.e1, a - {{0, -1}, {1, 0}}.e1};
  {g, h} = {b + d - a, b - d + a};
  {i, j} = {.8 d + .2 g, .8 g + .2 d};
  {k, l} = {i + f - d, j + f - d};
  axD = Norm[i - j]; axW = Norm[f - d];
  r1 = axD Cot[di]; r2 = r1/Cos[di]; r3 = axD Cot[di] + axW; 
  r4 = Sqrt[r3^2 + axD^2];
  Abs[(r1 + r3)/2]
  ]
  
Manipulate[
 d = {Cos[ArcTan @@ (a - b) - di], 
   Sin[ArcTan @@ (a - b) - 
     di]};(*the absolute orientation vector of the front wheel*)
 Framed@Graphics[{
    (*Parking marking*)
    {Thickness[.01], Line[{{-5.5, -3.2}, {-5.5, -.5}}]},
    Blue, Rectangle[{-6, -0.4}, {-5, 1.2}], FontSize -> Scaled[0.05], 
    Text[Style["P", "Title", Bold, White], {-5.5, 0.4}],
    (*Red walls*)
    {Red, Thickness[.01], 
     Table[Line[{{i, -1.15}, {i, -3}}], {i, -4, 2, 2}]},
    (*Car*)
    Opacity[.9], van[a, b, .2 d], Red, Arrow[{a, a + .5 fb (a - b)}],
    (*Wheel path*)
    circles[a, b, di], 
    wheelPathes = Join[wheelPathes, wheelPositions[a, b, .2 d]]; Red, 
    Point[wheelPathes],(*be care of:";"*)
    (*Path of car moving*)
    path = Append[path, (a + b)/2]; ColorData["DarkBands", 1], 
    Point[path]}, Background -> ColorData[13, 5], PlotRange -> 8, 
   ImageSize -> {1000, 800}], 
 Row[{Button["Try again", path = {}; wheelPathes = {};
    s = s + 1234; di = 0.5; fb = 1; SeedRandom[s];
    a = {RandomReal[{-2, 2}], RandomReal[{0, 2}]};
    t = RandomReal[{-\[Pi]/4., \[Pi]/4.}];
    b = a + 1.8 {Cos[t], Sin[t]};
    ImageSize -> Medium], Spacer[12];
   Button["Clear Path", path = {}; wheelPathes = {};
    ImageSize -> Medium], Spacer[12];
   Control[{{di, 0.1, "wheel"}, -\[Pi]/5, \[Pi]/5, Slider}], 
   Control[{{fb, 1, ""}, {1 -> " Forward ", -1 -> " Reverse "}}], 
   Spacer[12], 
   Button["Move", \[Omega] = 
     0.2/radious[a, b, di];(*change angluar speed based on radius*)
    rt = RotationTransform[-Sign[di] fb \[Omega], center[a, b, di]];
    a = rt[a]; b = rt[b]; t = t - Sign[di] fb \[Omega], 
    ImageSize -> Medium]}],
 {{a, {0, 1}}, None}, {{b, {0, -0.8}}, None}, {{t, -\[Pi]/6}, 
  None}, {{di, 0.5}, None}, {d, None}, {l1, None}, {l2, 
  None}, {\[Alpha], None}, {u, None}, {v, None}, {s, None}, {t, 
  None}, {a0, None}, {b0, None}, {\[Omega], None}, {rt, 
  None}, {{path, {}}, None}, {{wheelPathes, {}}, None}, 
 SaveDefinitions -> True, AutorunSequencing -> {1}]
 
 
 Manipulate[
 d = {Cos[ArcTan @@ (a - b) - di], 
   Sin[ArcTan @@ (a - b) - 
     di]};(*the absolute orientation vector of the front wheel*)
 Framed@Graphics[{
    (*Parking marking*)
    {Thickness[.01], Line[{{-5.5, -3.2}, {-5.5, -.5}}]},
    Blue, Rectangle[{-6, -0.4}, {-5, 1.2}], FontSize -> Scaled[0.05], 
    Text[Style["P", "Title", Bold, White], {-5.5, 0.4}],
    (*Red walls*)
    {Red, Thickness[.01], 
     Table[Line[{{i, -1.}, {i, -2.5}}], {i, -4, 9, 3.5}]},
    (*Car*)
    Opacity[.9], van[a, b, .2 d], Red, Arrow[{a, a + .5 fb (a - b)}],
    (*Wheel path*)
    circles[a, b, di], 
    wheelPathes = Join[wheelPathes, wheelPositions[a, b, .2 d]]; Red, 
    Point[wheelPathes],(*be care of:";"*)
    (*Path of car moving*)
    path = Append[path, (a + b)/2]; ColorData["DarkBands", 1], 
    Point[path]}, Background -> ColorData[13, 5], PlotRange -> 8, 
   ImageSize -> {1000, 800}], 
 Row[{Button["Try again", path = {}; wheelPathes = {};
    s = s + 1234; di = 0.5; fb = 1; SeedRandom[s];
    a = {RandomReal[{-2, 2}], RandomReal[{0, 2}]};
    t = RandomReal[{-\[Pi]/4., \[Pi]/4.}];
    b = a + 1.8 {Cos[t], Sin[t]};
    ImageSize -> Medium], Spacer[12];
   Button["Clear Path", path = {}; wheelPathes = {};
    ImageSize -> Medium], Spacer[12];
   Control[{{di, 0.1, "wheel"}, -\[Pi]/5, \[Pi]/5, Slider}], 
   Control[{{fb, 1, ""}, {1 -> " Forward ", -1 -> " Reverse "}}], 
   Spacer[12], 
   Button["Move", \[Omega] = 
     0.2/radious[a, b, di];(*change angluar speed based on radius*)
    rt = RotationTransform[-Sign[di] fb \[Omega], center[a, b, di]];
    a = rt[a]; b = rt[b]; t = t - Sign[di] fb \[Omega], 
    ImageSize -> Medium]}],
 {{a, {0, 1}}, None}, {{b, {0, -0.8}}, None}, {{t, -\[Pi]/6}, 
  None}, {{di, 0.5}, None}, {d, None}, {l1, None}, {l2, 
  None}, {\[Alpha], None}, {u, None}, {v, None}, {s, None}, {t, 
  None}, {a0, None}, {b0, None}, {\[Omega], None}, {rt, 
  None}, {{path, {}}, None}, {{wheelPathes, {}}, None}, 
 SaveDefinitions -> True, AutorunSequencing -> {1}]

Optimal Parking Situation

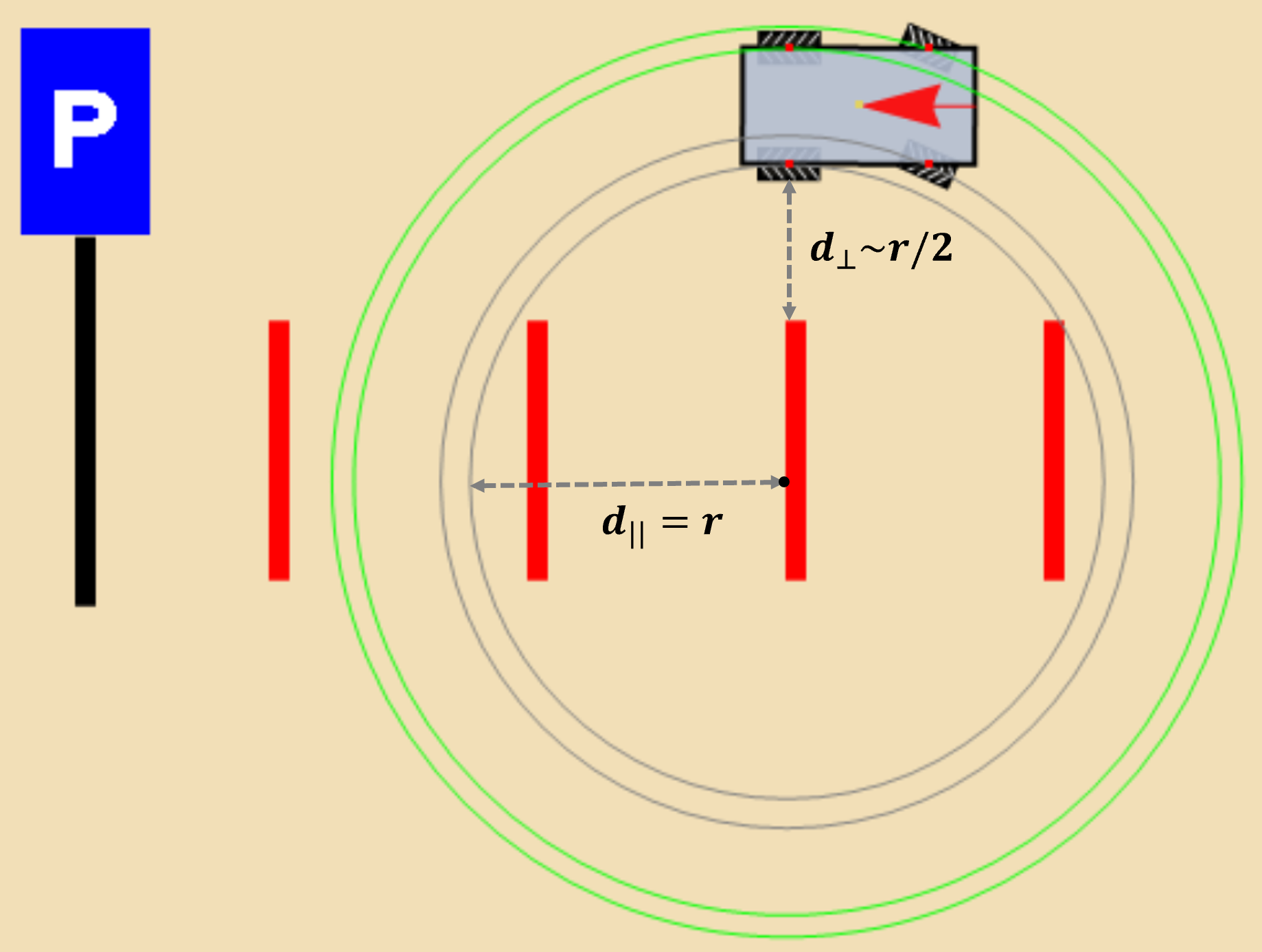
Perpendicular parking

Taking the minimal turning radius of the inner rear wheel as r, the optimal parking situation is shown in the image below. One should drive to a position where the parallel distance \(d_\parallel\) between the inner rear wheels at the initial and parking positions is close to \(r\). The pependicular distance \(d_\perp\) the inner rear wheel and the border of the parking space should be about \(r/2\)(as large as possible).

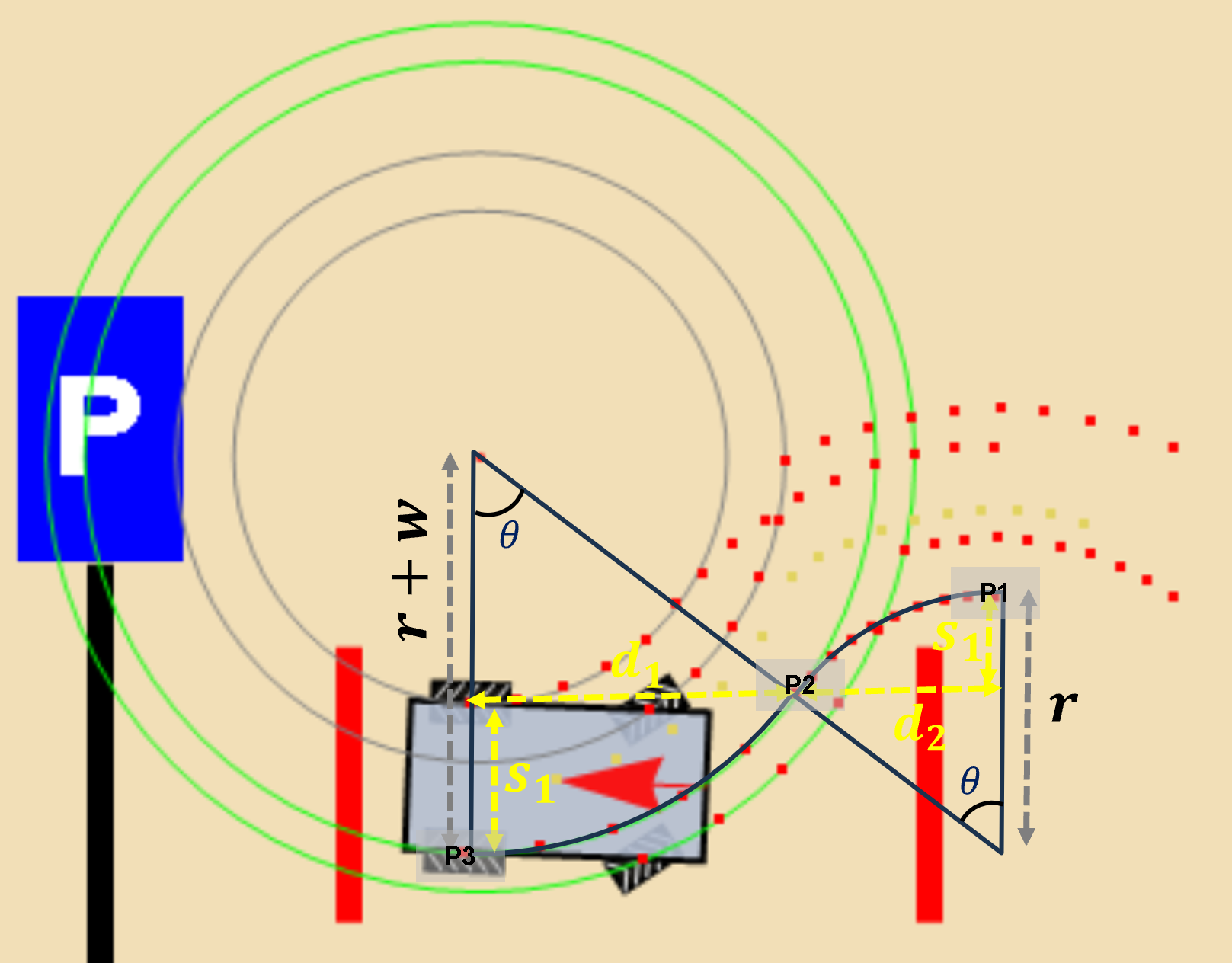
this is a placeholder image
Perpendicular parking with \(d_\parallel\) being the parallel distance between the inner rear wheels at the initinal and parked positions

Parallel parking

Parallel parking is a bit more complicated because it involves turning twice (ideally with equal-angle \(\theta\) turns). As shown in the image below, the rear wheel close to the parking space moves from P1 to P3 through P2, while the car remains parallel to the parking space in the end.

During this process, the total shift towards the parking place is \(s_1+s_2=r(1-\cos(\theta))+(r+w)(1-\cos(\theta))\) where \(w\) is the width of the vehicle, \(r\) the turning radius of the inner rear wheel. The distance reversed is \(d_1+d_2 = r\sin(\theta)+(r+w)\sin(\theta)\).

You can simply calculate the actually case for your cars.

this is a placeholder image
Perllel parking.

Summary

In this article, I shared my experience of getting a driving license in Germany and addresses the challenges of city parking. I explained car steering mechanics and use Mathematica visualizations to illustrate turning paths. Practical tips for are provided. Hope you get more confidence on parking now!

You May Also Enjoy